Les tentatives de l’expérience de Michelson pour mesurer la vitesse de la terre autour du soleil avec des rayons lumineux, qui ont échoué depuis plus d’un siècle, viennent d’être réussies par une autre méthode.
Michelson, jeune physicien américain, décida en 1881 de mesurer la vitesse de la terre autour du soleil en utilisant la règle de composition des vitesses.
Règle de la composition des vitesses
Sur une route droite (Figure 1), deux voitures A et B roulent en sens inverse l’une de l’autre, l’une à 70 km/heure, l’autre à 80 km/heure. La vitesse d’une voiture par rapport à l’autre est donc de 150 km/heure.

Si les deux voitures roulent dans le même sens (Figure 2), la vitesse de l’une par rapport à l’autre est de 10 km à l’heure, c’est à dire la différence de vitesse des deux voitures par rapport à la route.

Ainsi la règle de composition des vitesses permet lorsqu’on connaît deux des trois vitesses de calculer la troisième.
Si:
- va/r est la vitesse de a par rapport à la route
- vb/r la vitesse de b par rapport à la route r
- va/b la vitesse de a par rapport à b
on a les relations :
(1) va/b = vb/r + va/r
si les voitures roulent en sens inverse
(2) va/b = vb/r – va/r
si les voitures roulent dans le même sens
Expérience de Michelson
L’idée de Michelson était de comparer la vitesse des rayons lumineux allant en sens inverse du mouvement de la terre à celle de rayons lumineux allant dans une autre direction en utilisant les interférences découvertes par Young : si deux faisceaux lumineux de même origine se croisent après deux trajets différents, il apparaît dans la zone de croisement des raies claires et sombres. Si on supprime l’un des faisceaux, l’éclairage du croisement devient entièrement clair. Ce sont les raies sombres qui disparaissent. Young expliqua ce phénomène en supposant que la lumière était formée d’ondes lumineuses et non pas de grains comme on le croyait à cette époque.
En outre lorsqu’on change la longueur d’un des faisceaux, on observe un déplacement des franges. Ce déplacement est d’autant plus grand que le changement de longueur est plus grand. Ceci permet de mesurer le changement de longueur d’un faisceau avec une très grande précision.
Réalisation de l’expérience de Michelson
Un faisceau de lumière venant d’une source S (Figure 3) est envoyé sur un miroir B oblique à 45° par rapport au faisceau. Ce miroir est en partie transparent. Il renvoie la partie réfléchie du faisceau vers le miroir C et il est traversé par l’autre partie qui va vers le miroir D. Ces deux faisceaux sont réfléchis par les miroirs C et D qui les renvoient en B. Une partie du faisceau de D est réfléchie en B et poursuit son chemin vers l’écran E. Une partie du faisceau venant de C traverse B et poursuit son chemin vers l’écran E. Ces deux derniers faisceaux interfèrent et produisent des raies sombres et claires.
Dans un premier temps on oriente l’appareil de sorte que les rayons lumineux SB se dirigent en sens inverse du mouvement de la terre.
Si l’on nomme :
- vL1 la vitesse de la lumière quand les rayons lumineux se dirigent en sens inverse du mouvement de la terre
- vL la vitesse de la lumière au repos
- vT la vitesse de la terre
La vitesse de la lumière sera:
vL1 = vL + vT
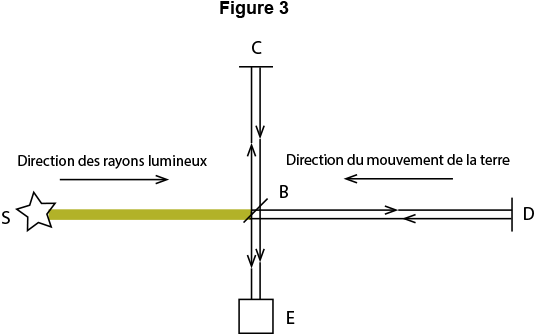
Puis on fait tourner l’appareil. La vitesse de la terre intervient différemment sur la vitesse mesurée de la lumière. Si la rotation est de 180°, la vitesse mesurée de la lumière est (relation 2):
vL2 = vL – vT
La vitesse de la terre est obtenue en soustrayant vL2 de vL1:
2 vT = vL1 – vL2
Michelson avait calculé que son appareil pouvait détecter des différences de vitesses de 3 km/sec. La vitesse de la terre étant de 30 km/sec, il ne doutait pas de son succès. Mais le résultat ne confirma ses espérances car il ne put observer le moindre déplacement des franges.
Cela signifiait que la vitesse de la lumière par rapport à la terre était la même dans le sens inverse du mouvement de la terre et dans le même sens
Surprise et embarras. Explications proposées
Tous les physiciens étaient surpris et embarrassés. C’était comme si dans les exemples des figures 1 et 2 la vitesse d’une automobile par rapport à l’autre était la même quand les deux automobiles allaient dans le même sens ou en sens inverse, comme si 150 km à l’heure était égal à 10 km à l’heure !
Michelson proposa que l’éther où se propage la lumière soit fixé à la terre comme l’atmosphère où se propage le son et on sait que celui-ci a la même vitesse dans toutes les directions. Mais Michelson, jeune physicien, se heurtait à l’opinion de l’époque d’un éther immobile qui avait été proposée par Fresnel et qui était soutenue par une expérience célèbre de Fizeau.
Fitzgerald en 1892 émit l’idée que si une différence de vitesses ne pouvait être observée dans l’expérience de Michelson, c’est que les longueurs des objets dans la direction de leur déplacement étaient raccourcies par le frottement de l’éther à cause de leur grande vitesse. Lorenz, qui avait eu en 1903 la même idée, fit observer que ce déplacement devait être d’autant plus important que leur vitesse était plus grande et il établit une relation donnant la nouvelle longueur des objets en fonction de leur vitesse:
\[l’ = l{\sqrt{1-{v^2\over c^2}}}\]- l’ étant la longueur des objets en mouvement
- l la longueur des objets au repos
- v la vitesse du déplacement des objets
- c la vitesse de la lumière
L’adhésion à cette hypothèse dura jusqu’à 1905, année où Einstein donna une autre explication dans la théorie de la relativité: Einstein demandait d’admettre deux postulats, c’est à dire deux propositions correspondant à des faits observés et acceptées pour vraies sans démonstration :
1- la vitesse de la lumière dans le vide est constante quelque soit le mouvement de l’observatoire où est faite la mesure;
2- les lois de la mécanique sont les mêmes dans deux observatoires différents quelque soit le mouvement de l’un par rapport à l’autre.
Le premier postulat traduit le résultat de l’expérience de Michelson: la vitesse de la lumière est la même quand on la mesure dans des directions différentes par rapport à la vitesse de la terre.
Le deuxième postulat permet à Einstein d’expliquer les différences de simultanéité dans un laboratoire en mouvement par rapport à un autre.
Il établit alors la relation entre les mesures faites dans les deux laboratoires. Cette relation était identique à celle établie par Lorenz.
L’avantage de l’explication d’Einstein sur celle de Fitzgerald et Lorenz est qu’il n’est pas nécessaire d’imaginer un frottement de l’éther sur les objets se déplaçant très rapidement. L’inconvénient est la difficulté à s’habituer à l’étrangeté de ses conséquences. Cela engendre des situations comme celle du paradoxe de Langevin: un astronome embarqué dans une fusée dont la vitesse serait 299 000 km par seconde et qui rentrerait sur Terre après un voyage qui, pour lui aurait duré deux ans, aurait la surprise de retrouver son frère jumeau, resté sur terre, vieilli de quarante ans. La vitesse des réactions chimiques qui conditionnent et entretiennent la vie aurait diminué de vingt fois .
Notons que l’explication de Fitzgerald et de Lorenz n’a pas été infirmée. C’est peut-être le charme dû à l’étrangeté des conclusions d’Einstein qui a retenu l’attention. Quoiqu’il en soit la théorie de la relativité est acceptée aujourd’hui par un très large public. Elle reste toutefois une hypothèse qui s’appuie sur deux postulats et le premier postulat repose sur l’échec de l’expérience de Michelson.
Mais cette expérience a été réussie au début de notre siècle en employant une autre méthode.
Réussite par une autre méthode de la tentative de Michelson de mesurer la vitesse de la Terre autour du Soleil avec des rayons lumineux
Cette méthode utilise:
- la spectrométrie
- l’effet Doppler Fizeau
- la variation de la vitesse des étoiles due au mouvement de leurs planètes
Cette dernière propriété a été très utilisée pour la recherche de planètes extrasolaire : l’observation directe des planètes extrasolaires est empêchée par l’éblouissement des étoiles hôtes, un milliard de fois plus lumineuses. En 1952, Otto Struve proposa de rechercher les planètes extrasolaires par la variation de vitesse d’éloignement des étoiles due à la révolution de leur planètes. En effet la révolution d’une planète, la terre par exemple, n’est que l’aspect le plus visible de la gravitation. Son étoile hôte, le soleil est également influencé par la terre. Il présente aussi une révolution qui peut être comparée au mouvement d’un athlète qui lance un marteau : celui-ci fait tourner le marteau pour augmenter sa vitesse mais il tourne aussi et ce n’est pas par coquetterie. Il s’incline spontanément du côté opposé au marteau car s’il ne le faisait pas il serait entraîné par lui et tomberait. Il est impossible de dissocier le mouvement du marteau de celui de l’athlète.
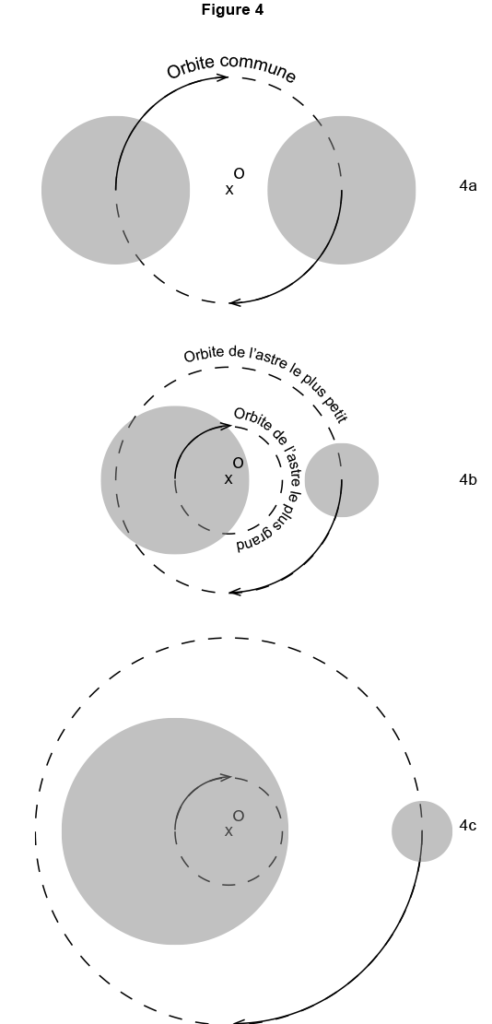
Cet effet existe pour tous les astres (figure 4)
Si deux astres de même masse tournent autour l’un de l’autre, ils tournent sur une même trajectoire autour d’un centre appelé centre de masse ou barycentre : O , en restant diamétralement opposés (figure 4a).
Si l’un est plus gros que l’autre (figure 4b),chacun des deux tourne autour du centre de masse O sur des orbites circulaires de rayons différents. L’orbite du plus gros a le rayon le plus petit.
Si la différence de masse est très importante (figure 4c) le centre de masse O peut être situé à l’intérieur de l’astre le plus gros. Le centre de masse du couple soleil – terre est situé tout près du centre du soleil. Le rayon de l’orbite du soleil est de 451 km, celui de la terre de 150 millions de km. La révolution du soleil est très petite en comparaison de celle de la terre et cependant elle suffit à modifier la vitesse d’éloignement du soleil par rapport aux autres étoiles et cette modification peut être mesurée avec les spectrographes actuels
En 1992, Alexandre Wolszczan découvrit que les éclairs d’un pulsar présentaient de très légères variations périodiques et il les attribua à la révolution d’une planète autour du pulsar.
En 1995, Mayor et Queloz réussirent à mettre en évidence par spectrométrie une variation périodique de la vitesse d’éloignement d’un « étoile normale », c’est à dire à luminosité constante et ils l’attribuèrent à la révolution d’une planète.
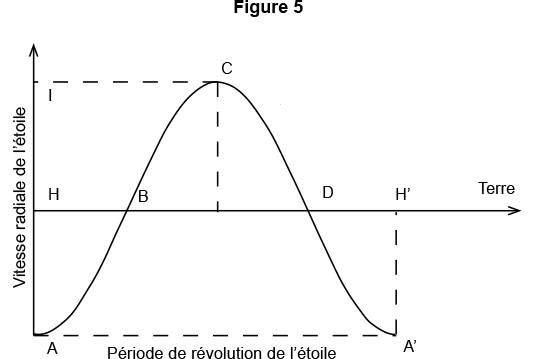
La figure 5 représente la variation de la vitesse radiale de l’étoile pendant une révolution autour du centre de masse:
- la courbe sinusoïdale représente cette variation
- HH’ est la période de révolution de l’étoile (et de la planète)
- H ordonnée de B et D correspond à la vitesse radiale moyenne d’éloignement de l’étoile
- I et A sont les valeurs des effets les plus importants de la vitesse de la planète sur sa vitesse d’éloignement moyenne. Ils correspondent à la vitesse de révolution de la planète.
Le succès de cette méthode a été immédiat. Dès le début du 21e siècle, plusieurs milliers de planètes extra-solaires ont ainsi été découvertes.
C’est une variante de cette méthode que deux auteurs, un enseignant d’astronomie I.A. Bonnel et un animateur anonyme du club d’astronomie du lycée Saint Exupéry de Lyon en août 2005, ont employée, pour mesurer, avec des rayons lumineux, la vitesse de la terre: leur originalité est de s’être servi de la révolution de la terre autour du soleil au lieu de la révolution d’une planète autour d’une étoile. Si la période de variation de cette vitesse est d’une année, la probabilité est grande que ce soit la terre qui en soit à l’origine.
I.A. Bonnel demandait à ses élèves, en travaux pratiques, de calculer la vitesse orbitale de la terre en mesurant le déplacement des raies du spectre d’Aldébaran, étoile située près du plan de l’écliptique. Les mesures devaient se répéter à intervalles réguliers pendant une année, période de révolution du soleil. Elles devaient être minutieuses, l’écart maximum attendu avec le spectrographe de l’université était de 3,0mm.
(https://www.st-andrews.ac.uk/~bds2/ltsn/planetary.rtf)
L’animateur du club d‘astronomie (https://cral-perso.univ-lyon1.fr/labo/fc/astrogebra/vot/TD/vot.pdf) demandait à ses lecteurs quelles étaient les conditions optimales d’observation pour mesurer la vitesse orbitale de la terre:
- choix de l’étoile ? Arcturus, parce qu’elle était proche du plan de l’écliptique
- périodes de l’année propices ?
- étalonnage des clichés ?
- mesures des décalages spectraux ?
- position de la terre et de l’étoile Arcturus au moment de la prise des clichés ?
La mesure par ces auteurs de la vitesse de la terre autour du soleil est remarquable, non-par la méthode qui avait déjà utilisée de nombreuses fois, mais par sa conséquence: Il contredit le premier postulat de la Théorie de la Relativité : « il est impossible sur la terre de mesurer la vitesse de celle-ci avec des rayons lumineux».
Ce postulat, qui s’appuie sur l’échec de l’expérience de Michelson et a été souvent confirmé en faisant la même expérience, est infirmé en employant une autre méthode de mesure
En résumé, pour mesurer la vitesse de la terre autour du soleil, il faut:
- choisir une étoile proche du plan de l’écliptique;
- construire la courbe sinusoïdale de la figure 4 de la vitesse d’éloignement de l’étoile
pendant une orbite complète du soleil (qui a la même durée qu’une orbite de la terre) - mesurer les écarts maximaux de cette vitesse (ordonnées de C et A) de la figure 4
avec la vitesse radiale d’éloignement des l’étoile (ordonnée de H) - Ces écarts sont égaux à la vitesse orbitale de la Terre.
La réussite de cette mesure remet en cause la Théorie de la Relativité.
Il y avait jusqu’ici en faveur de la théorie de la relativité l’échec répété de l’expérience de Michelson.
Contre elle, il y a maintenant la réussite de la méthode d’Otto Struve qui a été utilisée avec succès des milliers de fois.
Cet article est succinct. Des explications plus détaillées peuvent être trouvées dans un ouvrage intitulé:
La théorie de la Relativité perd son premier postulat
publié par La Simarre 1er trimestre 2022
ISBN : 978_2-36536-153-8
prix : 9 euros
Les techniques sont plus longuement expliquées et on y relève une erreur de Michelson dans l’application de la règle de composition des vitesses qui explique son résultat.