The attempts of Michelson’s experiment to measure the speed of the earth moving around the sun using light rays were not resolved for more than a century. This attempt has now been succeeded with another method.
At the end of the 19th century, Lord Kelvin wrote that physics was definitively constituted in its fundamental concepts; all it could further provide was the precise determination of a few more decimal places. Two problems remained: that of the black body and that of the negative result of Michelson’s experiment. He believed they would be quickly solved and did not alter our confidence in any way
Fortunately, he was wrong:
- Two of the most important discoveries in the field of physics were made only several months later: X-rays and radioactivity
- The two problems are still unresolved today: the black body remains an incomplete field of study, and Michelson’s experiment has been continually repeated and improved but has always failed.
Michelson had aimed to measure the speed of the earth moving around the sun using the rule of composition of speeds.
The rule of composition of speeds
Two cars A and B are travelling in opposite directions on a straight road A’B’ . (figure 1). One car is moving at 70 km/hour, the other at 80 km/hour. They reach point O at the same time. One hour before they were at A’ (70 km from O) and B’ (80 km from O), i.e. 150 km apart. This distance was reduced to 0 in one hour. Therefore, the speed of one car in relation to the other was 150 km per hour, i.e. the sum of the speeds of the two cars relative to the road [5].

If the two cars are travelling in the same direction (figure 2) and one catches up with the other at the point O’, one hour earlier they were at positions A” and B”, i.e. 10 km from A’’ to B’’. This distance was reduced to 0 in one hour. The speed of one car relative to the other was 10 km per hour, i.e. the difference in the speed of the two cars relative to the road.
Thus, when three speeds are involved, the rule of composition of speeds allows the third speed to be calculated if two of the three speeds are known.

If:
- va/r is the speed of A relative to the road;
- vb/r i the speed of B relative to the road;
- va/b is the speed of A relative to B.
we have the relationships:
(1) va/b = vb/r + va/r
if the cars are travelling in opposite directions.
(2) va/b = vb/r – va/r
if the cars are travelling in the same direction
If one car is travelling obliquely relative to the other (figure3) the result of the composition of speeds varies depending on the angle of the direction of car A with respect to that of car B.
It is equal to:
- vb/r + va/r when this angle is equal to 0
- vb/r when this angle is equal to 90°
- vb/r – va/r when this angle is equal to 180°
If v’1, v’2, v’3 are the projections of the speeds of cars A over the movement of car B and if these projections are in the opposite direction from the speed vB/R, the result of composition of speeds is increased with respect to the speed of car B, as is the case for v’1:
va/b + vb/r = v’1
If these projections are in the same direction as vB/R, the result of composition of speeds is reduced with respect to the speed of car B, as is the case for v’3.
va/b – vb/r = v’3
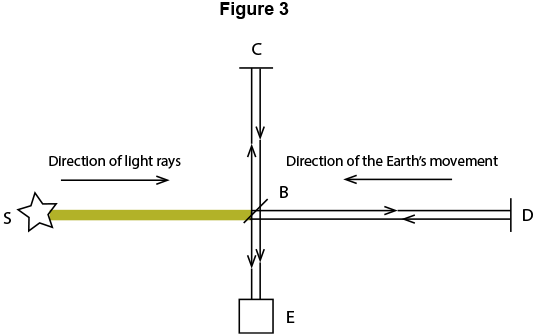
- v1, v2, v3: speeds of cars A with respect to the road for different directions of A/B;
- v’1, v’2, v’3: projections of speeds of cars A on the direction of vb/r
- vb/r: speed of car B with respect to the road
This difference in speed depending on the direction of movement of one car with respect to the other is best understood when the two cars come into contact. In the first case, when the cars are travelling in opposite directions, they crash and the drivers are killed. In the second case, when the cars are travelling in the same direction, their bumpers barely graze each other.
Michelson’s experiment
Michelson’s idea was to compare the speed of light rays travelling in the opposite direction to the movement of the earth to the speed of light rays travelling in another direction. For this, he used the interference discovered by Young: if two light beams from the same origin cross each other after taking two different paths, light and dark lines appear in the intersection area. If one of the beams is suppressed, the illumination of the intersection becomes completely clear. It is the dark lines that disappear! Young explained this phenomenon by presuming that light was made up of light waves and not of grains as was believed at that time.
Furthermore, when the length of one of the beams is altered, a displacement of the fringes is observed. The greater the change in length, the greater the displacement. This makes it possible to measure the alteration in the length of a beam with a very high degree of accuracy.
Carrying out the Michelson experiment
A beam of light from a source S (Figure 3) is directed onto a mirror, B, placed at an angle of 45° to the beam. This mirror is partly transparent. It directs the reflexive part of the beam back to mirror C and the rest of the beam passes through mirror B to mirror D. Both beams are reflected back to mirror B by mirrors C and D. Part of the beam from mirror D is reflected at B and continues on to screen E. Part of the beam from mirror C passes through B and continues on to screen E. These two beams interfere and produce the dark and light lines.
The first step is to orient the apparatus so that the SB light rays are directed in the opposite direction to the movement of the earth. The speed of light is given by:
vL1 = vL + vT
where:
- vL1 is the speed of light when the light rays are directed in the opposite direction to the movement of the earth
- vL is the speed of light at rest
- vT is the speed of the earth
Then the apparatus is rotated. The speed of the earth intervenes differently on the measured speed of light. If the rotation is 180°, the measured speed of light is (relation 2):
vL2 = vL – vT
The speed of the earth is calculated by subtracting vL2 from vL1
2 vT = vL1 – vL2
Michelson had calculated that his device could detect speed differences of 3 km/sec. The speed of the earth being 30 km/sec, he had no doubt of his success. But the result did not reach his expectations because he could not observe any displacement of the fringes.
This meant that the speed of light in relation to the earth was the same in the opposite direction to the earth’s movement as in the same direction!
Surprise and embarrassment. Proposed explanations
All physicists were surprised and embarrassed. It was as though in the examples in figures 1 and 2 the speed of one car in relation to the other was the same regardless of whether the two cars were going in the same direction or in the opposite direction. As though 150 km per hour was equal to 10 km per hour!
Michelson proposed that the ether through which light propagates should be fixed to the earth like the atmosphere through which sound propagates, and we know that sound has the same speed in all directions. But Michelson, a young physicist, came up against the opinion of the time of an immobile ether that had been proposed by Fresnel and which was supported by a famous experiment by Fizeau.
In 1892, Fitzgerald suggested that if no difference in velocity could be observed in Michelson’s experiment, it was because the lengths of the objects in the direction of their motion were shortened by the friction of the ether due to their high velocity. Lorenz had the same idea in 1903. He observed that the greater their speed, the greater this displacement must be, and he established a relationship giving the new length of the objects as a function of their speed:
\[l’ = l{\sqrt{1-{v^2\over c^2}}}\]Where:
- l’ is the length of objects in motion
- l is the length of the objects at rest
- v is the speed of the objects’ displacement
- c is the speed of light
Adherence to this hypothesis lasted until 1905, when Einstein gave an alternative explanation in his theory of relativity. Einstein asked that two postulates were admitted, i.e. two propositions corresponding to observed facts and accepted as true without demonstration:
1- the speed of light in a vacuum is constant whatever the movement of the observatory where the measurement is made;
2- the laws of mechanics are the same in two different observatories whatever the motion of one relative to the other.
The first postulate translates the result of Michelson’s experiment: the speed of light is the same when measured in different directions with respect to the movement of the earth.
The second postulate allows Einstein to explain differences in simultaneity of one moving laboratory compared to another.
Einstein then established the relationship between the measurements made in the two laboratories. This relationship was identical to that proposed by Lorenz.
The advantage of Einstein’s explanation over Fitzgerald’s and Lorenz’s is that it is not necessary to imagine ether friction on the fast-moving objects. The disadvantage is that it is difficult to become used to the strangeness of its consequences. This leads to situations such as the Langevin paradox: an astronomer returning to Earth after a journey lasting two years in a rocket travelling at 299,000 km per second would be surprised to find his twin brother, who had remained on Earth, would have aged by forty years. The speed of the chemical reactions that condition and sustain life would have decreased twenty-fold.
It should be noted that Fitzgerald’s and Lorenz’s explanation has never been overturned. Perhaps it was the charm of Einstein’s conclusions because of their strangeness that attracted attention. In any case, the theory of relativity is accepted today by a very large public. However, it remains a hypothesis based on two postulates and the first postulate is based on the failure of the Michelson experiment.
But this experiment succeeded at the beginning of our century using another method.
Success of Michelson’s attempt to measure the speed of the Earth around the Sun by another method with light rays
This method uses:
- spectrometry
- the Doppler Fizeau effect
- the variation in the speed of stars due to the motion of their planets
This last property has been widely used in the search for extrasolar planets. The direct observation of extrasolar planets is prevented by the glare of the host stars, which are a billion times brighter than the planets. In 1952, Otto Struve proposed the use of the variation in the velocity of the stars due to the revolution of their planets to search for extra-solar planets. Indeed, the revolution of a planet, Earth for example, is only the most visible aspect of gravitation. Its host star, the sun, is also influenced by Earth. It also has a revolution that can be compared to the movement of an athlete throwing a hammer. The athlete spins the hammer to increase his speed, but he himself spins and this is not for coquetry. He spontaneously bends to the side opposite the hammer because if he did not, he would be dragged down by it and fall. It is impossible to dissociate the movement of the hammer from that of the athlete.
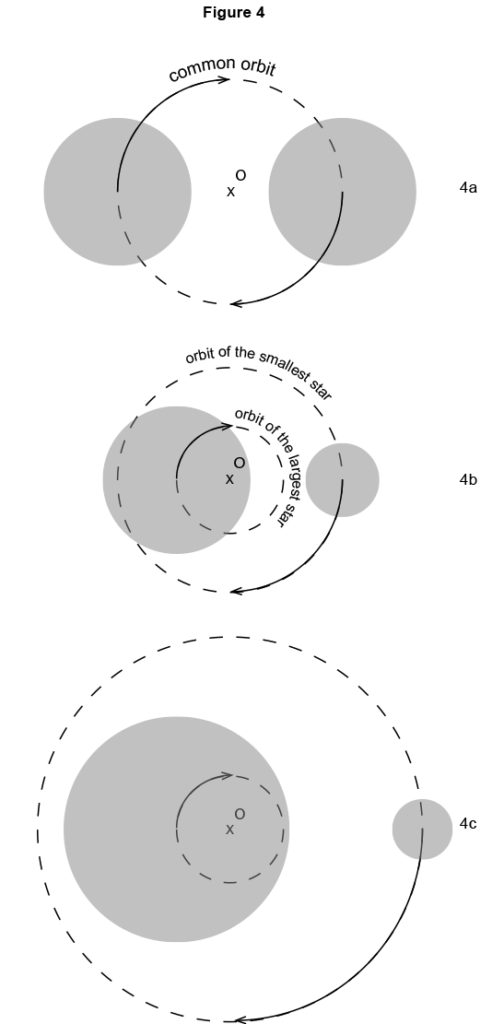
This effect exists for all stars (figure 4)
If two stars of the same mass revolve around each other, they revolve on the same trajectory around a centre called the centre of mass or barycentre: O, while remaining diametrically opposed (figure 4a).
If one star is larger than the other (figure 4b), they both revolve around the centre of mass O in circular orbits of different radii. The orbit of the larger star has the smaller radius.
If the difference in mass is very large (figure 4c), the centre of mass O may be located inside the larger star. The centre of mass of the sun-Earth pair is located very close to the centre of the sun. The radius of the sun’s orbit is 451 km and that of Earth is 150 million km. The revolution of the sun is very small compared to that of Earth and yet it is sufficient to modify the speed of the sun’s distance from the other stars and this modification can be measured with current spectrographs
In 1992, Alexandre Wolszczan discovered that the flashes of a pulsar show very slight periodic variations and he attributed these to the revolution of a planet around the pulsar.
In 1895, Mayor and Queloz succeeded in demonstrating by spectrometry a periodic variation in the radial velocity of a ‘normal star’, i.e. one with constant luminosity, and they attributed this variation to the revolution of a planet.
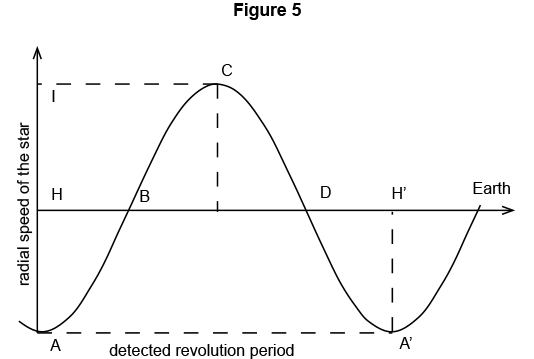
Figure 5 shows the variation of the radial velocity of the star during a revolution around the centre of mass:
- the sine curve represents this variation;
- HH’ is the period of revolution of the star (and of the planet);
- H is the ordinate of B and D is the mean radial velocity of the star;
- I and A are the values of the most important effects of the planet’s velocity on its mean distancing velocity. They correspond to the planet’s speed of revolution.
The success of this method was immediate. By the beginning of the 21st century, several thousand extra-solar planets had been discovered.
In August 2005, two authors, an astronomy teacher I.A. Bonnel and an anonymous organizer of the astronomy club of the Saint Exupéry high school in Lyon, used a variant of this method to measure the speed of the earth with light rays. Their originality is that they used the revolution of Earth around the sun in their studies, instead of the revolution of a planet around a star. If the period of variation of this speed is one year, the probability is high that Earth is at the origin.
I.A. Bonnel asked his students to calculate the Earth’s orbital velocity by measuring the displacement of lines in the spectrum of Aldebaran, a star located near the ecliptic plane. The measurements were to be repeated at regular intervals over the course of a year, the sun’s period of revolution. They had to be meticulous, with a maximum expected deviation of 3.0 mm from the university’s spectrograph. (https://www.st-andrews.ac.uk/~bds2/ltsn/planetary.rtf)
The host of the astronomy club (https://cral-perso.univ-lyon1.fr/labo/fc/astrogebra/vot/TD/vot.pdf) asked his readers what the optimal observing conditions are for measuring the Earth’s orbital velocity:
the choice of star? Arcturus surely, because of its proximity to the ecliptic plane;
- the best periods of the year?
- image calibration?
- measurements of spectral shifts?
- position of the earth and the star Arcturus at the time the images were taken?
The measurement of the speed of the earth around the sun by these authors is remarkable : This contradicts the first postulate of the Theory of Relativity: “from the Earth it is impossible to measure its speed with light rays.”
This postulate, which is based on the failure of Michelson’s experiment and was often confirmed by repeating the same experiment, was invalidated by using another measurement method
In summary, to measure the speed of the earth around the sun, one must:
- choose a star close to the ecliptic plane;
- construct the sine curve shown in Figure 4 of the star’s velocity as it moves
away from the sun during a complete orbit of the sun (which has the same duration as an orbit of Earth) - measure the maximum deviations of this velocity (ordinates of C and A)
as in figure 4 from the radial velocity of the star (ordinate of H)
These deviations are equal to the orbital speed of the Earth.
The success of this measurement calls into question the Theory of Relativity.
In favour of the Theory of Relativity was the repeated failure of the Michelson experiment.
Against this theory, there is now the achievement of Otto Struve’s method which has been used successfully thousands of times.
This article is concise. More detailed explanations can be found in a book entitled:
La théorie de la Relativité perd son premier postulat
published by La Simarre 1er trimestre 2022
ISBN : 978_2-36536-153-8
price : 9 euros
The techniques are explained at greater length and Michelson’s error in the application of the velocity composition rule is noted which explains his result.